目录
二分模板
两大基本原则
- 每次都要缩减搜索区域
- 每次缩减不能排除潜在答案
模板 1
找一个准确值
- 循环条件:
l <= r - 缩减搜索空间:
l = mid + 1, r = mid - 1
def binarySearch(nums, target):
l, r = 0, len(nums)-1
while l <= r:
mid = l + (r - l)//2
if nums[mid] == target:
return mid # 返回索引
elif target < nums[mid]:
r = mid - 1
else:
l = mid + 1
return -1
模板 2
找一个模糊值
- 循环条件:
l < r - 缩减搜索空间:
l = mid, r = mid - 1或者l = mid + 1, r = mid
def fuzzy_search_small(nums, target):
l, r = 0, len(nums) - 1
while l < r:
mid = l + (r - l + 1)//2
if nums[mid] < target:
l = mid
else:
r = mid - 1
return nums[l] if nums[l] < target else -1
def fuzzy_search_big(nums, target):
l, r = 0, len(nums) - 1
while l < r:
mid = l + (r - l) // 2
if nums[mid] <= target:
l = mid + 1
else:
r = mid
return nums[l] if nums[l] > target else -1
模板 3
万用型
- 循环条件:
l < r - 1 - 缩减搜索空间:
l = mid, r = mid
def fuzzy_search(nums, target):
l, r = 0, len(nums)-1
while l < r - 1:
mid = l + (r-l)//2
if nums[mid] == target:
return [mid] # 返回索引
elif nums[mid] < target:
l = mid
else:
r = mid
tmp = nums[l]/2.0 + nums[r]/2.0 # 中间值
if target == tmp:
return [l, r]
elif target < tmp:
return [l]
else:
return [r]
每日一题
69. x 的平方根
https://leetcode-cn.com/problems/sqrtx/
题目描述
Note
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入: 4
输出: 2
示例 2:
输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
思路
- 解 $\sqrt{n} \leq \frac{n}{2}$:
- $n = 0$,
return 0 - $1 \leq n \leq 3$,
return 1 - $n \geq 4$, 满足 $\sqrt{n} \leq \frac{n}{2}$
- $n = 0$,
- 在 $\left[1, n//2\right]$ 内二分
- 利于除法判断:
mid > x/mid, 避免溢出
代码
Python
class Solution:
def mySqrt(self, x: int) -> int:
if x == 0: return 0
i, j = 1, x // 2
while i < j:
mid = i + (j-i+1) // 2
if mid > x/mid:
j = mid - 1
else:
i = mid
return i
复杂度
- 时间复杂度:$O(logX)$
- 空间复杂度:$O(1)$
278. 第一个错误的版本
https://leetcode-cn.com/problems/first-bad-version/
题目描述
Note
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5,并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
思路
- 简单二分思路
- 相当于二元递增数组
[0, 0, 0, 1, 1] - 找到第一个
1
代码
Python
# The isBadVersion API is already defined for you.
# @param version, an integer
# @return an integer
# def isBadVersion(version):
class Solution:
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
i, j = 1, n
while i < j:
mid = i + (j-i) // 2
if isBadVersion(mid):
j = mid
else:
i = mid + 1
return i
复杂度
- 时间复杂度:$O(logN)$
- 空间复杂度:$O(1)$
Triple Inversion
https://binarysearch.com/problems/Triple-Inversion
题目描述
Note
Given a list of integers nums, return the number of pairs i < j such that nums[i] > nums[j] * 3.
Constraints
n ≤ 100,000wherenis the length ofnums
Example
- Input
nums = [7, 1, 2] - Output
2 - Explanation
We have the pairs (7, 1) and (7, 2)
思路
- 构造递增数组
d - 借助 bisect 模块,边插入边排序
代码
Python
class Solution:
def solve(self, nums):
res, d = 0, []
for num in nums:
idx = bisect.bisect_right(d, 3*num) # 返回最右侧索引
res += len(d) - idx
bisect.insort(d, num)
return res
复杂度
- 时间复杂度:$O(n^2)$
- 空间复杂度:$O(n)$
Minimum-Light-Radius
https://binarysearch.com/problems/Minimum-Light-Radius
题目描述
Note
思路
代码
Python
复杂度
- 时间复杂度:
- 空间复杂度:
推荐题目
33. 搜索旋转排序数组
https://leetcode-cn.com/problems/search-in-rotated-sorted-array/
题目描述
Note
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, $[0,1,2,4,5,6,7]$ 在下标 $3$ 处经旋转后可能变为 $[4,5,6,7,0,1,2]$
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target,则返回它的索引,否则返回 $-1$
示例 1:
输入: $nums = [4,5,6,7,0,1,2], \ target = 0$
输出: $4$
示例 2:
输入: $nums = [4,5,6,7,0,1,2], \ target = 3$
输出: $-1$
示例 3:
输入: $nums = [1],\ target = 0$
输出: $-1$
提示:
- $1 \leq nums.length \leq 5000$
- $-10^4 \leq nums[i] \leq 10^4$
nums中的每个值都 独一无二nums肯定会在某个点上旋转- $-10^4 \leq target \leq 10^4$
思路
- 二分法,每次必须缩小区间,不能去掉可能解
nums[left] <= nums[mid]$\Longrightarrow$ 左侧为有序序列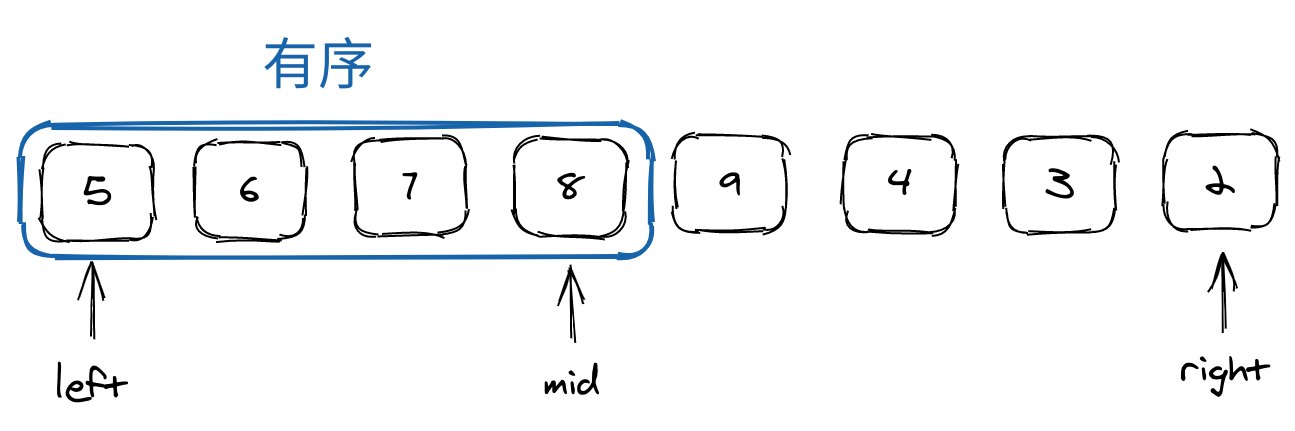
nums[left] > nums[mid]$\Longrightarrow$ 右侧为有序序列
代码
Python
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums)-1
while left <= right:
mid = left + (right-left)//2
if nums[mid] == target: return mid
if nums[left] <= nums[mid]: # 左侧为有序序列
if nums[left] <= target < nums[mid]:
right = mid-1
else:
left = mid+1
else: # 右侧为有序序列
if nums[mid] < target <= nums[right]:
left = mid+1
else:
right = mid-1
return -1
复杂度
- 时间复杂度:$O(logN)$
- 空间复杂度:$O(1)$
81. 搜索旋转排序数组 II
https://leetcode-cn.com/problems/search-in-rotated-sorted-array-ii/
题目描述
Note
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 $[0,0,1,2,2,5,6]$ 可能变为 $[2,5,6,0,0,1,2]$ )。
编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true,否则返回 false。
示例 1:
输入: nums = [2,5,6,0,0,1,2], target = 0
输出: true
示例 2:
输入: nums = [2,5,6,0,0,1,2], target = 3
输出: false
思路
- 相对于 33. 搜索旋转排序数组,本题中元素可能重复
while left < mid and nums[left] == nums[mid]: # 消除重复元素
left += 1
代码
Python
class Solution:
def search(self, nums: List[int], target: int) -> bool:
left, right = 0, len(nums)-1
while left <= right:
mid = left + (right-left)//2
if nums[mid] == target: return True
while left < mid and nums[left] == nums[mid]:
left += 1 # 消除重复元素
if nums[left] <= nums[mid]: # 左侧为有序序列
if nums[left] <= target < nums[mid]:
right = mid-1
else:
left = mid+1
else: # 右侧为有序序列
if nums[mid] < target <= nums[right]:
left = mid+1
else:
right = mid-1
return False
复杂度
- 时间复杂度:$O(logN)$
- 空间复杂度:$O(1)$